7  Análisis de datos inferencial

---

Paquetes para este capítulo

if (!require('afex')) install.packages('afex'); library('afex')
if (!require('correlation')) install.packages('correlation'); library('correlation')
if (!require('corrr')) install.packages('corrr'); library('corrr')
if (!require('cowplot')) install.packages('cowplot'); library('cowplot')
if (!require('dplyr')) install.packages('dplyr'); library('dplyr')
if (!require('gapminder')) install.packages('gapminder'); library('gapminder')
if (!require('ggplot2')) install.packages('ggplot2'); library('ggplot2')
if (!require('ggridges')) install.packages('ggridges'); library('ggridges')
if (!require('gtsummary')) install.packages('gtsummary'); library('gtsummary')
if (!require('haven')) install.packages('haven'); library('haven')
if (!require('inspectdf')) install.packages('inspectdf'); library('inspectdf')
if (!require('knitr')) install.packages('knitr'); library('knitr')
if (!require('lme4')) install.packages('lme4'); library('lme4')
if (!require('papaja')) install.packages("papaja"); library('papaja')
if (!require('parameters')) install.packages('parameters'); library('parameters')
if (!require('performance')) install.packages('performance'); library('performance')
if (!require('report')) install.packages('report'); library('report')
if (!require('sjPlot')) install.packages('sjPlot'); library('sjPlot')
if (!require('tidyr')) install.packages('tidyr'); library('tidyr')

---

7.1 Análisis de datos y reporte de resultados

R es un lenguaje creado por estadísicos que ha ido evolucionando hacia un lenguaje de programación completo. No obstante, una de sus fortalezas innegables es el análisis de datos, y el reporte de resultados. En esta sección vamos a ver de manera muy general algunas de las herramientas que tenemos a nuestra disposición.

7.1.1 Tablas

Hay numerosos paquetes para crear tablas descriptivas o para facilitar el reporte de resultados en R:

• {gtsummary}
  
• {stargazer}
  
• {papaja}
  
• {flextable}
  
• {huxtable}

Mostraremos algunos ejemplos usando gtsummary. Una ventaja interesante es que permite de manera sencilla transformar nuestra tabla a otros formatos.

7.2 Tablas descriptivos

Podemos crear tablas con los descriptivos de nuestros datos usando la función tbl_summary() de {gtsummary}

# Por defecto, usa: mediana (rango inter cuartil)
gapminder |> 
  select(-country) |> 
  gtsummary::tbl_summary() 

Characteristic	N = 1,704 1
continent
Africa	624 (37%)
Americas	300 (18%)
Asia	396 (23%)
Europe	360 (21%)
Oceania	24 (1.4%)
year	1,980 (1,965, 1,995)
lifeExp	61 (48, 71)
pop	7,023,596 (2,792,776, 19,593,661)
gdpPercap	3,532 (1,202, 9,326)
1 n (%); Median (Q1, Q3)

Usando el parámetro by podemos crear columnas para cada valor de una variable:

# Por continente 
gapminder |> 
  select(-country) |> 
  gtsummary::tbl_summary(by = continent)

Characteristic	Africa N = 624 1	Americas N = 300 1	Asia N = 396 1	Europe N = 360 1	Oceania N = 24 1
year	1,980 (1,965, 1,995)	1,980 (1,965, 1,995)	1,980 (1,965, 1,995)	1,980 (1,965, 1,995)	1,980 (1,965, 1,995)
lifeExp	48 (42, 54)	67 (58, 72)	62 (51, 70)	72 (70, 75)	74 (71, 78)
pop	4,579,311 (1,341,536, 10,822,313)	6,227,510 (2,959,572, 18,555,489)	14,530,831 (3,830,365, 46,426,880)	8,551,125 (4,329,000, 21,947,137)	6,403,492 (3,187,775, 14,629,150)
gdpPercap	1,192 (761, 2,378)	5,466 (3,426, 7,853)	2,647 (1,057, 8,565)	12,082 (7,190, 20,477)	17,983 (13,820, 22,539)
1 Median (Q1, Q3)

El parámetro statistic nos permite controlar que estadísticos mostrar en función del tipo de variable. En el caso de abajo, usaremos “promedio (desviación estándar)” para las variables continuas y “número de observaciones (% del total)” para las variables categóricas.

gapminder |> 
  select(-country) |> 
  gtsummary::tbl_summary(by = continent,
                         statistic = list(all_continuous() ~ "{mean} ({sd})",
                                          all_categorical() ~ "{n} ({p}%)"),
                       missing = "ifany") |> 
  gtsummary::add_n() |> 
  gtsummary::modify_spanning_header(c("stat_1", "stat_2", "stat_3", "stat_4", "stat_5") ~ "**Continent**")

Characteristic	N	Continent
		Africa N = 624 1	Americas N = 300 1	Asia N = 396 1	Europe N = 360 1	Oceania N = 24 1
year	1,704	1,980 (17)	1,980 (17)	1,980 (17)	1,980 (17)	1,980 (18)
lifeExp	1,704	49 (9)	65 (9)	60 (12)	72 (5)	74 (4)
pop	1,704	9,916,003 (15,490,923)	24,504,795 (50,979,430)	77,038,722 (206,885,205)	17,169,765 (20,519,438)	8,874,672 (6,506,342)
gdpPercap	1,704	2,194 (2,828)	7,136 (6,397)	7,902 (14,045)	14,469 (9,355)	18,622 (6,359)
1 Mean (SD)

Ejercicio - Descriptivos

Usando la base de datos del apartado anterior:

DF_dafina = haven::read_sav(here::here("data/files/Dafina", "Cancer screening risk literacy R1.sav")) |> as_tibble() |> 
  select(IDparticipante, resident, screenbeliefs, compR1, numeracy) |>  
  rename(comprehension = compR1) 

Intenta reproducir la tabla de abajo. En el manual de gtsummary tienes ejemplos para todo lo que necesitarás. Busca a la función tbl_summary().

La tabla me muestra demasiado detalle, pero sólo quiero los promedios

Si todas tus variables son continuas, puedes usar type = list(everything() ~ 'continuous'), dentro de tbl_summary() para forzar el tratamiento de variables con pocos niveles como continuas.

Error al añadir valor p

En la ayuda de la función: ?add_p.tbl_summary encontrarás que puedes usar algo como: add_p(test = everything() ~ "t.test")

¿Cómo consigo poner el titulo Resident?

Fíjate cómo usamos modify_spanning_header() en el ejemplo anterior. Solo tienes que adaptarlo a los datos actuales, donde tenemos únicamente dos grupos.

Characteristic	N	Resident		p-value 2
		0 N = 54 1	1 N = 118 1
IDparticipante	172	72 (51)	93 (48)	0.012
Screening beliefs	172	27.4 (5.0)	28.4 (6.8)	0.3
Comprehension of the evidence	172	2.91 (1.28)	2.54 (1.16)	0.077
Numeracy BNT-S	172	3.70 (1.54)	2.87 (1.56)	0.001
1 Mean (SD)
2 Welch Two Sample t-test

---

7.3 Tablas resultados inferenciales

Para tablas con los resultados de nuestros modelos estadísticos, usamos la función tbl_regression() de {gtsummary}

Primero preparamos los datos:

# Transform variables
DF_gapminder = gapminder |> 
  # Log
  mutate(gdpPercap_log = log(gdpPercap),
         pop_log = log(pop)
         ) |> 
  # Mean center variables so the 0 values have meaning
  mutate(year = year - mean(year, na.rm = TRUE),
         gdpPercap_log = gdpPercap_log - mean(gdpPercap_log, na.rm = TRUE),
         pop_log = pop_log - mean(pop_log, na.rm = TRUE)) |> 
  # Will use only last year
  filter(year == max(year))

Creamos un modelo sencillo y mostramos la tabla de resultados.

model1 = lm(lifeExp ~ gdpPercap_log + pop_log, DF_gapminder)

table_model1 = gtsummary::tbl_regression(model1, intercept = TRUE) |> 
  add_global_p() |>
  bold_labels() |> 
  italicize_levels() |> 
  add_glance_table(include = c("nobs", "df.residual", "r.squared", "adj.r.squared"))


table_model1

Characteristic	Beta	95% CI 1	p-value
(Intercept)	63	62, 65	<0.001
gdpPercap_log	7.2	6.4, 8.1	<0.001
pop_log	0.81	0.04, 1.6	0.039
No. Obs.	142
Residual df	139
R²	0.665
Adjusted R²	0.660
1 CI = Confidence Interval

7.4 Reporte de resultados

Con la función report() podemos ver una descripción completa de los resultados de nuestro modelo:

  report::report(model1)
#> We fitted a linear model (estimated using OLS) to predict lifeExp with
#> gdpPercap_log and pop_log (formula: lifeExp ~ gdpPercap_log + pop_log). The
#> model explains a statistically significant and substantial proportion of
#> variance (R2 = 0.66, F(2, 139) = 137.93, p < .001, adj. R2 = 0.66). The
#> model's intercept, corresponding to gdpPercap_log = 0 and pop_log = 0, is at
#> 63.28 (95% CI [61.98, 64.58], t(139) = 96.30, p < .001). Within this model:
#> 
#>   - The effect of gdpPercap log is statistically significant and positive
#> (beta = 7.24, 95% CI [6.38, 8.11], t(139) = 16.56, p < .001; Std. beta =
#> 0.81, 95% CI [0.72, 0.91])
#>   - The effect of pop log is statistically significant and positive (beta =
#> 0.81, 95% CI [0.04, 1.58], t(139) = 2.09, p = 0.039; Std. beta = 0.10, 95%
#> CI [5.35e-03, 0.20])
#> 
#> Standardized parameters were obtained by fitting the model on a standardized
#> version of the dataset. 95% Confidence Intervals (CIs) and p-values were
#> computed using a Wald t-distribution approximation.

7.5 Texto inline

Algo genial de gtsummary, es que podemos usar las propias tablas para extraer detalles de los resultados y usarlos directamente en el texto.

El paquete report tiene también funcionalidades muy potentes que merece la pena explorar.

La ventaja de escribir los resultados de esta manera es que si hacemos algún pequeño cambio en la preparación de datos, podemos volver a correr el script de generación del reporte de resultados, y los valores p, etc. se ajustarán automáticamente. Únicamente tenemos que asegurarnos que la interpretación cualitativa no cambia :)

paste0(
  "Life expectancy was significantly associated with GDP per capita (log), beta = ",
  gtsummary::inline_text(table_model1, variable = gdpPercap_log)
)  
#> [1] "Life expectancy was significantly associated with GDP per capita (log), beta = 7.2 (95% CI 6.4, 8.1; p<0.001)"

Ejercicio - Resultados inferenciales

Usando la misma base de datos del ejercicio anterior:

DF_dafina = haven::read_sav(here::here("data/files/Dafina/Cancer screening risk literacy R1.sav")) |>
  as_tibble() |>
  select(IDparticipante, resident, screenbeliefs, compR1, numeracy) |>
  rename(comprehension = compR1) 

Haz una regresión lineal prediciendo comprensión a partir de las otras variables de la base.

Finalmente, crea una tabla similar a la siguiente para reportar los resultados de tu análisis. Recuerda que en el manual de gtsummary tienes ejemplos para todo lo que necesitarás. En concreto, tbl_regression() es tu amiga:

Funciones necesarias

add_global_p() para los valores p. bold_labels() para poner en negrita los nombres de variables

Como añadir información en el pie de la tabla

Tendrás que usar la función add_glance_source_note() o add_glance_table(). Para saber que nombres poner en el parámetro include, puedes usar la función broom::glance(model), donde model es el nombre que has usado para tu modelo estadístico.

Characteristic	Beta	95% CI 1	p-value
(Intercept)	2.8	1.9, 3.8
Resident	-0.23	-0.62, 0.17	0.3
Screening beliefs	-0.02	-0.05, 0.01	0.2
Numeracy BNT-S	0.14	0.03, 0.26	0.016
No. Obs. = 172; Adjusted R² = 0.047; Residual df = 168; Statistic = 3.83; p-value = 0.011; df = 3
1 CI = Confidence Interval

---

7.6 Unir tablas

De manera muy sencilla podemos unir varias tablas. Esto es útil, por ejemplo, para mostrar los resultados de regresiones jerárquicas:

# Primero creamos un modelo más sencillo, basado en el anterior
model10 = lm(lifeExp ~ gdpPercap_log, DF_gapminder)

# Creamos la tabla
table_model10 = gtsummary::tbl_regression(model10, intercept = TRUE) |>
  add_global_p() |>
  bold_labels() |>
  italicize_levels() |>
  add_glance_table(include = c("nobs", "df.residual", "r.squared", "adj.r.squared"))

# Combinamos ambas tablas
tbl_merge(
  tbls = list(table_model10, table_model1),
  tab_spanner = c("**Baseline**", "**Step 1**")) |> 
  # Necesario para que los parámetros globales de los modelos se muestren al final
  modify_table_body(~.x |> arrange(row_type == "glance_statistic")
  )

Characteristic	Baseline			Step 1
	Beta	95% CI 1	p-value	Beta	95% CI 1	p-value
(Intercept)	64	62, 65	<0.001	63	62, 65	<0.001
gdpPercap_log	7.2	6.3, 8.1	<0.001	7.2	6.4, 8.1	<0.001
pop_log				0.81	0.04, 1.6	0.039
No. Obs.	142			142
Residual df	140			139
R²	0.654			0.665
Adjusted R²	0.652			0.660
1 CI = Confidence Interval

7.7 Otros análisis y sus tablas

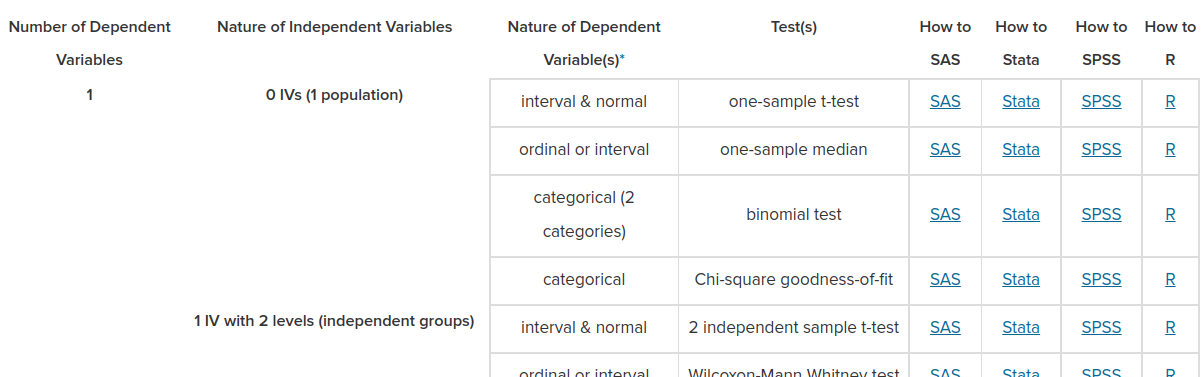
Que test estadístico debería usar, con código en R

---

7.7.1 Correlación simple

# Data
iris |> as_tibble()
#> # A tibble: 150 × 5
#>   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#>          <dbl>       <dbl>        <dbl>       <dbl> <fct>  
#> 1          5.1         3.5          1.4         0.2 setosa 
#> 2          4.9         3            1.4         0.2 setosa 
#> 3          4.7         3.2          1.3         0.2 setosa 
#> 4          4.6         3.1          1.5         0.2 setosa 
#> 5          5           3.6          1.4         0.2 setosa 
#> 6          5.4         3.9          1.7         0.4 setosa 
#> # ℹ 144 more rows

# Test
simple_corr_test = cor.test(iris$Sepal.Width, iris$Sepal.Length, method = "spearman")

# Report
simple_corr_test |> report::report()
#> Effect sizes were labelled following Funder's (2019) recommendations.
#> 
#> The Spearman's rank correlation rho between iris$Sepal.Width and
#> iris$Sepal.Length is negative, statistically significant, and small (rho =
#> -0.17, S = 6.56e+05, p = 0.041)

7.7.2 Multiples correlaciones

# Multiple correlations
table_correlations = iris |> 
  correlation(partial = FALSE, method = "spearman")

# Print table
TABLE_CORR = table_correlations |> 
  summary(stars = FALSE, include_significance = TRUE, p_digits = 3) 

# Fancy table
TABLE_CORR |> 
  parameters::print_md()

Correlation Matrix (spearman-method)

Parameter	Petal.Width	Petal.Length	Sepal.Width
Sepal.Length	0.83 (p < .001)	0.88 (p < .001)	-0.17 (p = 0.041)
Sepal.Width	-0.29 (p < .001)	-0.31 (p < .001)
Petal.Length	0.94 (p < .001)

p-value adjustment method: Holm (1979)

7.7.3 Anova

• Ver paquete {afex}

data(obk.long, package = "afex")
head(obk.long)
#>   id treatment gender   age phase hour value
#> 1  1   control      M -4.75   pre    1     1
#> 2  1   control      M -4.75   pre    2     2
#> 3  1   control      M -4.75   pre    3     4
#> 4  1   control      M -4.75   pre    4     2
#> 5  1   control      M -4.75   pre    5     1
#> 6  1   control      M -4.75  post    1     3

# estimate mixed ANOVA on the full design:
model = afex::aov_ez(id = "id", 
                     dv = "value", 
                     data = obk.long, between = c("treatment"), 
        within = c("phase", "hour"))

  
  table_afex = papaja::apa_print(model)$table
  knitr::kable(table_afex)

term	estimate	conf.int	statistic	df	df.residual	p.value
Treatment	.211	[.000, .468]	2.91	2	13	.090
Phase	.164	[.000, .356]	19.29	1.74	22.64	< .001
Hour	.129	[.000, .237]	18.44	1.95	25.41	< .001
Treatment \(\times\) Phase	.099	[.000, .212]	5.43	3.48	22.64	.004
Treatment \(\times\) Hour	.001	[.000, .000]	0.08	3.91	25.41	.987
Phase \(\times\) Hour	.017	[.000, .000]	1.35	4.02	52.29	.265
Treatment \(\times\) Phase \(\times\) Hour	.008	[.000, .000]	0.33	8.05	52.29	.951

7.7.4 Modelos mixtos

Primero preparamos los datos:

# Transform variables
DF_gapminder2 = gapminder |> 
  # Log
  mutate(gdpPercap_log = log(gdpPercap),
         pop_log = log(pop)
         ) |> 
  # Mean center variables so the 0 values have meaning
  mutate(year = year - mean(year, na.rm = TRUE),
         gdpPercap_log = gdpPercap_log - mean(gdpPercap_log, na.rm = TRUE),
         pop_log = pop_log - mean(pop_log, na.rm = TRUE))

# Reference levels and contrast coding
DF_gapminder2 <- within(DF_gapminder2, continent <- relevel(continent, ref = "Oceania"))
contrasts(DF_gapminder2$continent) = car::contr.Sum(levels(DF_gapminder2$continent))

Creamos un modelo sencillo:

model2 = lme4::lmer(lifeExp ~ gdpPercap_log + pop_log + year + (1|country), DF_gapminder2)

# Extraemos los R2 del modelo para usar en la tabla
R2_1 = performance::r2(model2)
  

Y mostramos la tabla de resultados. Como se trata de modelos mixtos, tenemos que añadir manualmente los R2’s.

table_model2 = gtsummary::tbl_regression(model2) |>  #, intercept = TRUE
  add_global_p() |>
  bold_labels() |>
  italicize_levels() |>
  add_glance_source_note(include = c("nobs", "df.residual"))

# broomExtra::glance_performance(model2)

table_model2 |> 
  as_gt() |> 
  gt::tab_source_note(gt::md(
    paste0(
      deparse1(model2@call$formula),
      "<BR> ",
      "R2 conditional = ",
      round(R2_1$R2_conditional, 3),
      ", R2 marginal = ",
      round(R2_1$R2_marginal, 3)
    )
  ))

Characteristic	Beta	95% CI 1	p-value
gdpPercap_log	3.3	2.8, 3.8
pop_log	6.1	5.4, 6.9
year	0.15	0.13, 0.17
No. Obs. = 1,704; Residual df = 1,698
lifeExp ~ gdpPercap_log + pop_log + year + (1 | country) R2 conditional = 0.964, R2 marginal = 0.49
1 CI = Confidence Interval

Bibliografía

Wickham, H., & Grolemund, G. (2016). R for data science: import, tidy, transform, visualize, and model data. O’Reilly Media, Inc. https://r4ds.had.co.nz/